Top 7 Evaluation of Functions Examples with Solutions
-
Bella Williams
- 10 min read
Function evaluation examples serve as practical tools for grasping mathematical concepts. Through these examples, we engage with diverse functions, unraveling their mechanics and applications. Evaluating functions enhances our problem-solving skills and aids in developing a deeper understanding of algebraic principles.
In this section, we will explore seven compelling examples of function evaluation, each accompanied by detailed solutions. These examples will illuminate the evaluation process, demonstrating how to input values into functions and interpret results effectively. By the end of this exploration, readers will feel more confident in applying function evaluation to real-world scenarios.
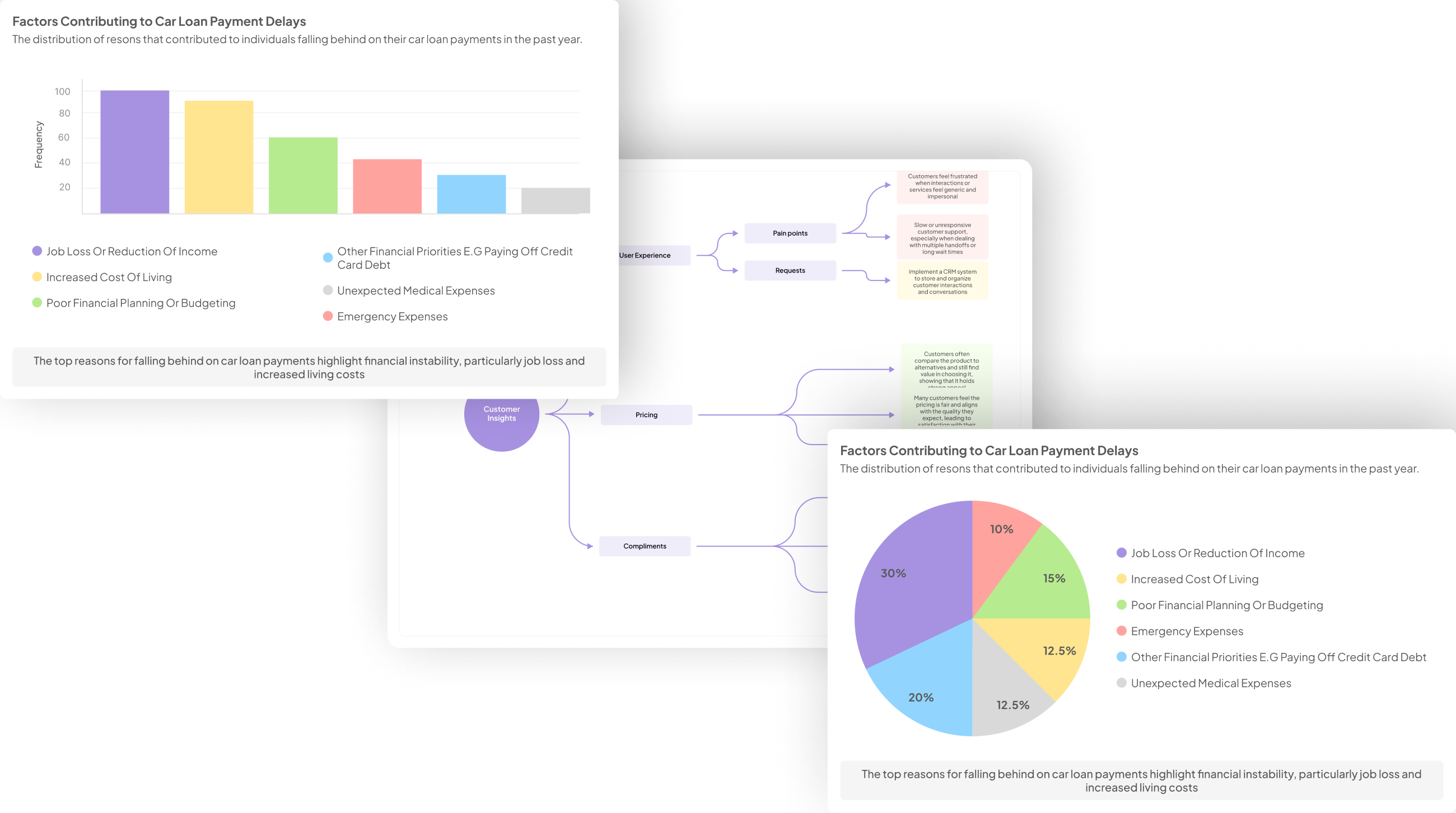
Generate visualizations from your qualitative data. At Scale.
The Importance of Function Evaluation Examples
Function evaluation examples serve as a critical tool in understanding how mathematical concepts apply in real-world scenarios. By illustrating different types of functions through clear examples, learners can grasp abstract concepts more effectively. Whether dealing with linear, quadratic, or exponential functions, examples allow students to visualize and apply these theoretical ideas in practical situations.
Moreover, evaluating these functions equips learners with essential problem-solving skills. Each example demonstrates the step-by-step process of calculating function values, enhancing confidence and competence in tackling similar problems. This process not only builds foundational knowledge but also prepares students for more advanced topics. Therefore, engaging with function evaluation examples is invaluable for solidifying comprehension and fostering a deeper appreciation for mathematics in everyday life.
Overview of Function Evaluation
Function evaluation is a fundamental concept in mathematics that allows us to determine the output of a function for a given input. By substituting specific values into a function’s equation, we can explore how functions behave. Understanding function evaluation examples is essential for mastering more complex mathematical concepts later on. This foundational skill also aids in problem-solving across various real-world scenarios.
To grasp function evaluation effectively, it is beneficial to consider several key examples. First, we can examine linear functions, where outputs change at a constant rate. Second, quadratic functions illustrate how outputs can change relative to the square of the input. Third, exponential functions demonstrate rapid growth patterns. Each of these examples highlights different behavior types, making it simpler to engage with function evaluation. By analyzing these examples and their solutions, learners can build a solid understanding of function evaluation and its applications.
Real-World Applications of Function Evaluation
Function evaluation examples play a significant role in our everyday decisions and activities. For instance, consider financial planning, where evaluating functions can help forecast savings over time based on monthly contributions and interest rates. By plugging specific values into a mathematical function, individuals can determine how much they will have saved by a certain date. This process offers clarity on reaching financial goals.
Another practical application of function evaluation is in the realm of data science. Here, professionals use functions to analyze trends in consumer behavior. By inputting data points into a function, analysts can derive insights that inform business strategies and marketing campaigns. Understanding these real-world function evaluation examples allows us to appreciate their impact across various fields, from personal finances to corporate decision-making. Moreover, mastering these evaluations equips individuals with essential skills needed in today’s data-driven environment.
Mathematics in Action: Function Evaluation Examples
Understanding function evaluation examples is crucial for grasping the fundamentals of mathematics. These examples vividly illustrate how to compute values based on different inputs, promoting a deeper understanding of functions. By examining specific cases, learners can see how various mathematical expressions yield different outcomes when particular values are plugged in.
To delve into function evaluation examples, consider the following steps. First, identify the function you need to evaluate, noting its mathematical expression. Second, substitute the specific input values into the function. Finally, calculate the result to see how the function behaves with different inputs. This process demonstrates how functions act within mathematical contexts and highlights their practical applications in real-world scenarios. Engaging with these evaluations not only sharpens computation skills but also nurtures critical thinking abilities essential for advanced mathematical studies.
Solving Algebraic Equations
Solving algebraic equations is a fundamental skill in mathematics, often applied to evaluate functions. When engaging with function evaluation examples, it’s essential to grasp how to isolate variables to find their values. For instance, to solve an equation like (2x + 4 = 12), we first need to eliminate the constant by subtracting 4 from both sides. This step simplifies the equation to (2x = 8). From here, dividing both sides by 2 reveals (x = 4).
Understanding the properties of algebraic operations is crucial in this process. Additionally, recognizing how to transpose equations helps in evaluating different functions. Using examples, such as (f(x) = x^2 – 5), we evaluate by substituting values for (x) to derive corresponding outputs. Mastering these strategies establishes a strong foundation for solving complex equations and enhances one’s problem-solving skills in function evaluation contexts.
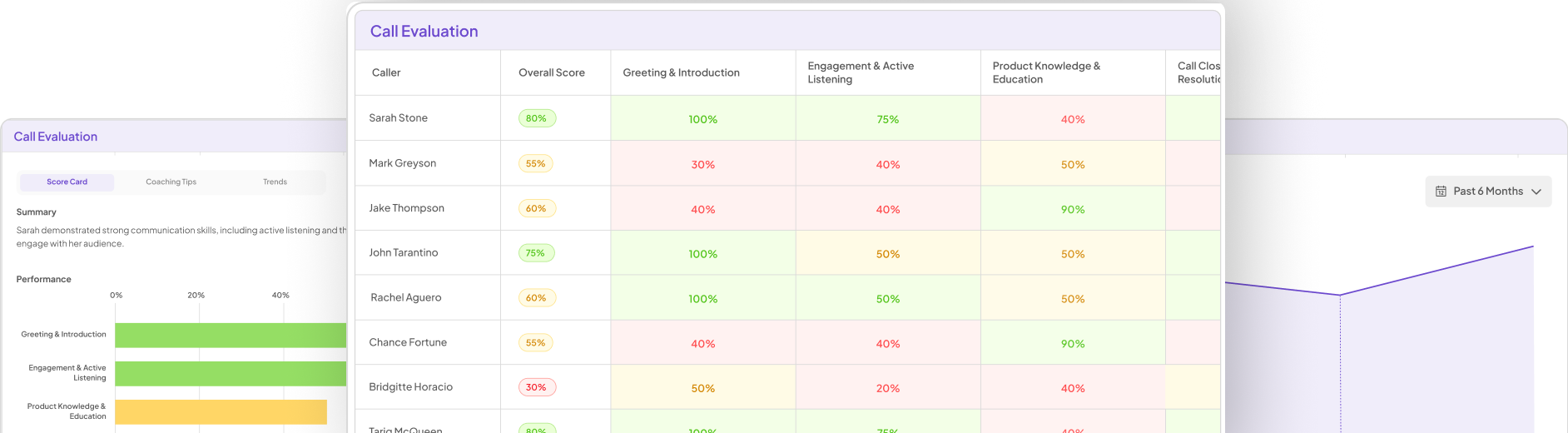
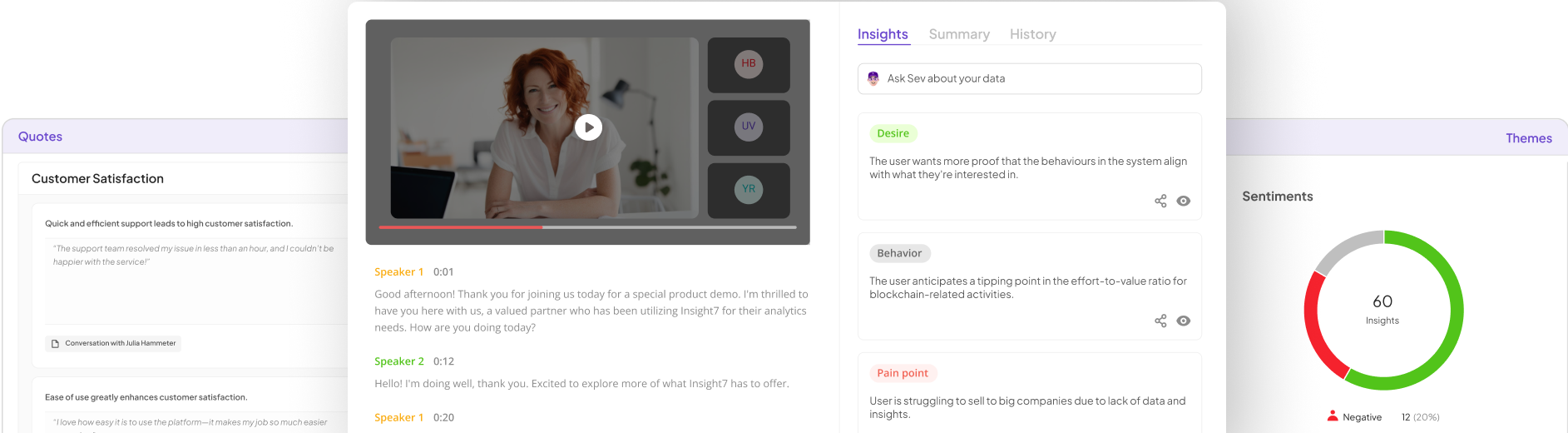
Evaluate Performance on Customer Calls for Quality Assurance.
Real-Life Problem Solving with Functions
Real-life problem solving with functions often involves translating complex scenarios into simpler equations. Understanding how to evaluate functions can provide valuable insights in various fields, from healthcare logistics to customer service. By exploring function evaluation examples, we can see how mathematical solutions directly impact decision-making processes.
For instance, consider a scenario where a logistics team needs to determine optimal flight routes for families. By using a function to represent travel times as a variable, evaluating it for different routes can lead to efficient airport selections. Additionally, if certain options are unavailable, having alternative functions ready for evaluation allows quick adjustments, ensuring that families receive the care they need. This problem-solving approach not only streamlines operations but also enhances overall satisfaction by providing timely support.
Step-by-Step Guide to Function Evaluation Examples
Function evaluation examples provide a clear way to understand how to apply mathematical expressions for specific inputs. In this section, you will gain insights into various methods of evaluating functions step by step. Each example illustrates different types of functions and how to approach them analytically. This structured approach allows for a deeper understanding of concepts such as domain, range, and functional relationships.
To facilitate your comprehension, we will highlight each example numerically. First, we will demonstrate evaluating a linear function. Next, we will explore quadratic functions and their unique characteristics. Third, we will look at polynomial functions, analyzing their behavior with different inputs. Following that, we’ll evaluate exponential functions for insight into their rapid growth. Fifth, the focus will be on logarithmic functions, crucial for understanding inverse relationships. We will then tackle trigonometric functions and their periodic nature. Lastly, we will assess piecewise functions, which showcase how functions can behave differently based on the input range. By following these steps, you’ll gain practical skills in function evaluation that will enhance your mathematical proficiency.
Evaluating Polynomial Functions
Evaluating polynomial functions involves determining the output of a polynomial expression for specific input values. This process is essential for understanding how polynomials behave and how they can be applied in various mathematical contexts. By substituting values into the polynomial, we can find the corresponding results, which helps to visualize the function’s graph and analyze its properties.
To illustrate this concept, let’s consider a few examples. First, evaluate (f(x) = 2x^2 + 3x – 5) at (x = 1). By substituting, we get (f(1) = 2(1)^2 + 3(1) – 5 = 0). Second, evaluate the same polynomial at (x = -2). This time, (f(-2) = 2(-2)^2 + 3(-2) – 5 = -1). These function evaluation examples illustrate how to compute polynomial values step-by-step and underline the significance of evaluation in comprehending polynomials.
Example with Solutions: Quadratic Functions
Quadratic functions play a vital role in essential mathematical concepts and their evaluation. When working with these functions, one can gain valuable insights through function evaluation examples. For instance, consider the quadratic function (f(x) = ax^2 + bx + c). To evaluate this function for specific values of (x), simply substitute the number into the equation. This straightforward substitution showcases how changes in (x) influence the outcome.
To illustrate this further, let’s evaluate (f(x) = 2x^2 – 3x + 5) for (x = 2).
Applying Concepts to Cubic Functions
Applying concepts to cubic functions allows us to explore how these mathematical expressions behave under various conditions. To make sense of their characteristics, we can evaluate different function examples. Function evaluation examples for cubic functions reveal their unique features, such as turning points and intercepts, which can be crucial in mathematical modeling or real-world applications.
Consider these pivotal aspects when applying concepts to cubic functions: first, identify the leading coefficient, which influences the graph’s direction. Second, recognize the roots or zeros, where the function crosses the x-axis. Finally, examine critical points derived from the first derivative, which indicate local maxima or minima. Understanding these elements can enhance your grasp of cubic functions and their behavior in various scenarios, offering valuable insights for practical problem-solving.
Generate visualizations from your qualitative data. At Scale.

Conclusion: Mastery of Function Evaluation Examples
Mastering function evaluation examples is essential for anyone looking to understand mathematics better. Throughout this document, a variety of function evaluation examples have been thoroughly explored and solved. Each example highlights the step-by-step process required to arrive at the correct answers, building your confidence and problem-solving skills along the way.
By engaging with these function evaluation examples, you are likely to enhance your analytical abilities. This newfound mastery can pave the way for tackling more complex mathematical concepts in the future. Embrace these examples as a stepping stone on your journey toward mathematical proficiency, as they illustrate practical applications that will serve you well in any advanced study.