Introduction to Monte Carlo Policy Evaluation in Research
-
Bella Williams
- 10 min read
Stochastic Value Estimation plays a crucial role in refining Monte Carlo Policy Evaluation. This method applies probabilistic techniques to assess policies effectively, enabling researchers to understand potential outcomes from various decision-making processes. As a valuable approach in uncertain environments, it allows analysts to simulate numerous scenarios while maintaining a comprehensive view of policy performance within complex systems.
With Stochastic Value Estimation, traditional evaluation frameworks transform into dynamic tools capable of adapting to varying conditions. Researchers can harness the power of Monte Carlo sampling to gather insights and evaluate policies over time, thus achieving a more accurate value estimate. This approach enhances the decision-making process, fostering a deeper comprehension of how different policies can influence outcomes in real-world applications.
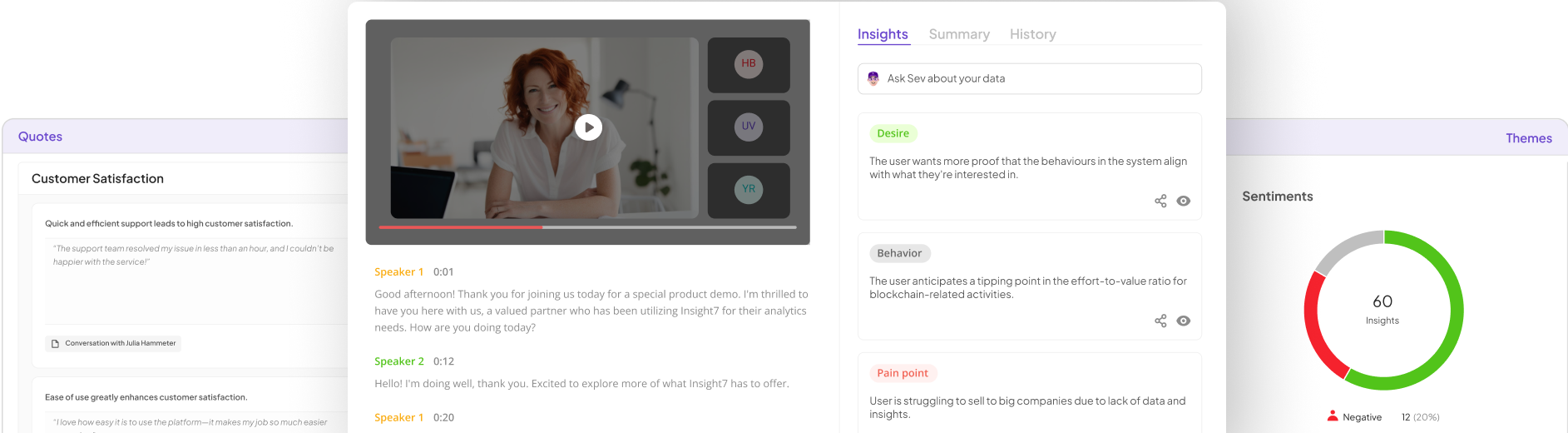
Generate visualizations from your qualitative data. At Scale.
Foundations of Monte Carlo Methods in Stochastic Value Estimation
Monte Carlo methods serve as a robust framework for stochastic value estimation by harnessing randomness to approximate metrics of interest. In essence, these methods utilize random sampling to generate outcomes that reveal insights about expected returns in various scenarios. Specifically, stochastic value estimation involves calculating the expected values associated with different actions in uncertain environments. This means that rather than deriving a fixed value, practitioners can analyze a range of potential outcomes.
At the core of Monte Carlo methods is their ability to tackle complex problems where traditional analytical tools may falter. To achieve this, the procedure typically follows key steps: sampling, evaluation, and aggregation. First, a series of random samples are drawn from the probability distribution of unknown variables. Next, these samples are evaluated through simulations to compute their respective outcomes. Finally, the results are aggregated to estimate the overall value, providing a comprehensive view of the variability inherent in stochastic environments. This combination of sampling and analysis underlines the practical utility of Monte Carlo methods in the context of stochastic value estimation.
Historical Background and Development
Monte Carlo methods have their roots in the early 20th century, primarily as tools for statistical analysis and computational simulations. Researchers sought improved techniques for dealing with uncertainty in complex systems, leading to the emergence of concepts that now underpin Stochastic Value Estimation. As computational power increased, these methods became practical for evaluating policies across various fields, including finance, engineering, and artificial intelligence.
The development of Monte Carlo Policy Evaluation reflects a progression toward more sophisticated approaches in assessing decision-making processes under uncertainty. Over time, the integration of algorithmic techniques and data analysis has played a pivotal role in refining these methods. By providing a framework to simulate different scenarios, Monte Carlo Policy Evaluation allows for a deeper understanding of potential outcomes and informs strategic decisions effectively. The evolution of this approach signifies the broader acceptance and recognition of Stochastic Value Estimation in research contexts.
Core Concepts and Principles
Stochastic Value Estimation is the cornerstone of Monte Carlo Policy Evaluation. This approach relies on random sampling to estimate the value of different actions in a decision-making process. By simulating various scenarios, researchers can gain insights into how different strategies might perform over time. This is particularly beneficial in complex environments where traditional analytical methods may fall short.
Key principles of Stochastic Value Estimation include understanding the concept of randomness and its implications for value assessment. Firstly, it is crucial to grasp that each sampled scenario may yield different outcomes, which reflects the inherent uncertainty in decision-making. Secondly, the law of large numbers emphasizes that with sufficient samples, the average of the results will converge to the expected value, providing a more reliable estimate. Lastly, designing experiments that efficiently explore the state space can significantly enhance estimation accuracy. All these principles work together to facilitate informed decision-making in uncertain conditions.
Stochastic Value Estimation: Applying Monte Carlo Policy Evaluation
Stochastic Value Estimation plays a vital role in understanding the effectiveness of different policies within a stochastic environment. This process utilizes Monte Carlo Policy Evaluation, which estimates the value of a policy by sampling episodes that follow a specific strategy. By generating multiple trajectories of state-action sequences, researchers can capture the inherent randomness and variability present in the environment, allowing for more robust predictions.
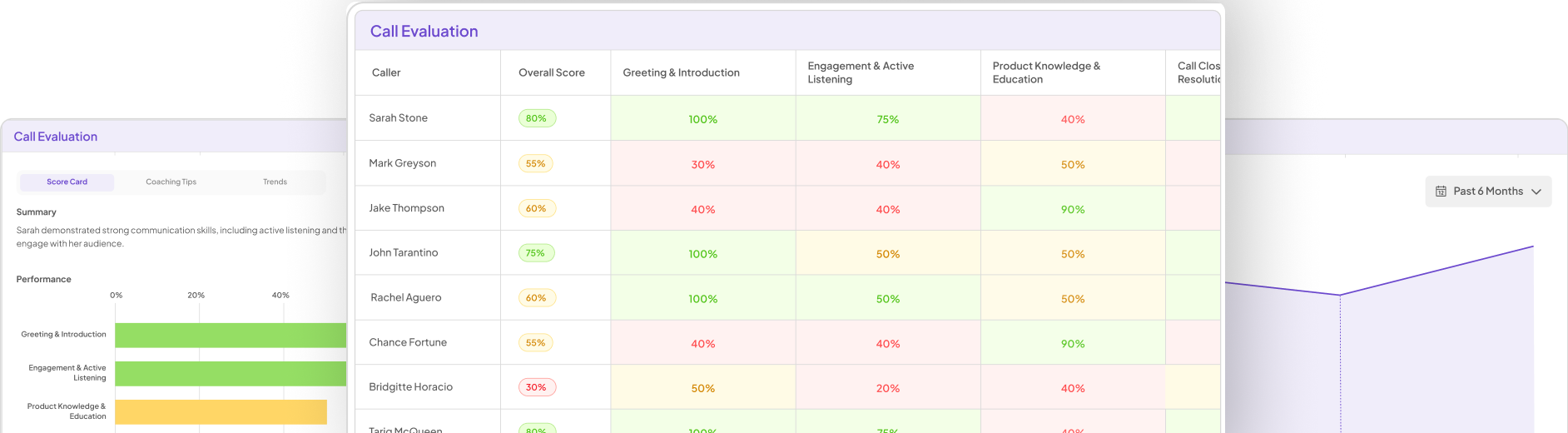
Evaluate Performance on Customer Calls for Quality Assurance.
The Monte Carlo method aggregates the results from various simulations to calculate an average value for each state. This technique is particularly beneficial for scenarios where the environment is complex and uncertain. As it allows for the evaluation of policies without requiring a complete model, practitioners can make data-driven decisions based on the empirical results gathered from their simulations. By applying this method, organizations can understand policy performance and optimize their strategies in changing conditions.
Implementation Techniques and Strategies
To effectively implement Stochastic Value Estimation in Monte Carlo Policy Evaluation, several key techniques and strategies must be considered. First, data collection plays a crucial role; having rich, high-quality data enables accurate value assessments. This ensures that the Monte Carlo simulations are based on realistic scenarios, which enhance the reliability of the outcomes.
Next, appropriate sampling methods are essential for the validity of the evaluations. Random sampling techniques, such as uniform and stratified sampling, maximize the diversity of outcomes acquired from the simulations. Additionally, implementing variance reduction techniques, including control variates and importance sampling, can significantly improve estimation accuracy.
It’s also vital to establish a robust computational framework to handle the simulations efficiently. This can involve optimizing algorithms and leveraging distributed computing resources for handling larger data sets. By understanding these implementation techniques and strategies, researchers can effectively harness Stochastic Value Estimation in their Monte Carlo analyses.
Case Studies and Applications in Research
Case studies in research utilizing Stochastic Value Estimation illuminate the practical applications of this theoretical framework. Researchers have employed Monte Carlo methods to evaluate policies in diverse fields, from finance to healthcare. One notable example is the use of these methods in optimizing treatment protocols in clinical trials. By simulating various treatment scenarios, researchers can assess potential outcomes, improving patient outcomes through data-driven decisions.
Another significant application lies in reinforcement learning. Researchers have implemented Stochastic Value Estimation to train agents in complex environments, enhancing their decision-making processes. These practical examples demonstrate the versatility of Monte Carlo Policy Evaluation techniques, showcasing how they can be adapted to solve real-world challenges. Ultimately, the insights gleaned from these case studies highlight the capacity of these methods to provide reliable estimates that inform critical choices across multiple sectors.
Conclusion: Advancements and Future Prospects in Stochastic Value Estimation
Stochastic Value Estimation has made significant advancements in recent years, shaping how researchers approach policy evaluation. With the integration of sophisticated algorithms and data analysis techniques, the accuracy of value estimates has improved remarkably. These developments empower decision-makers with reliable insights, ultimately leading to more effective strategies across various sectors.
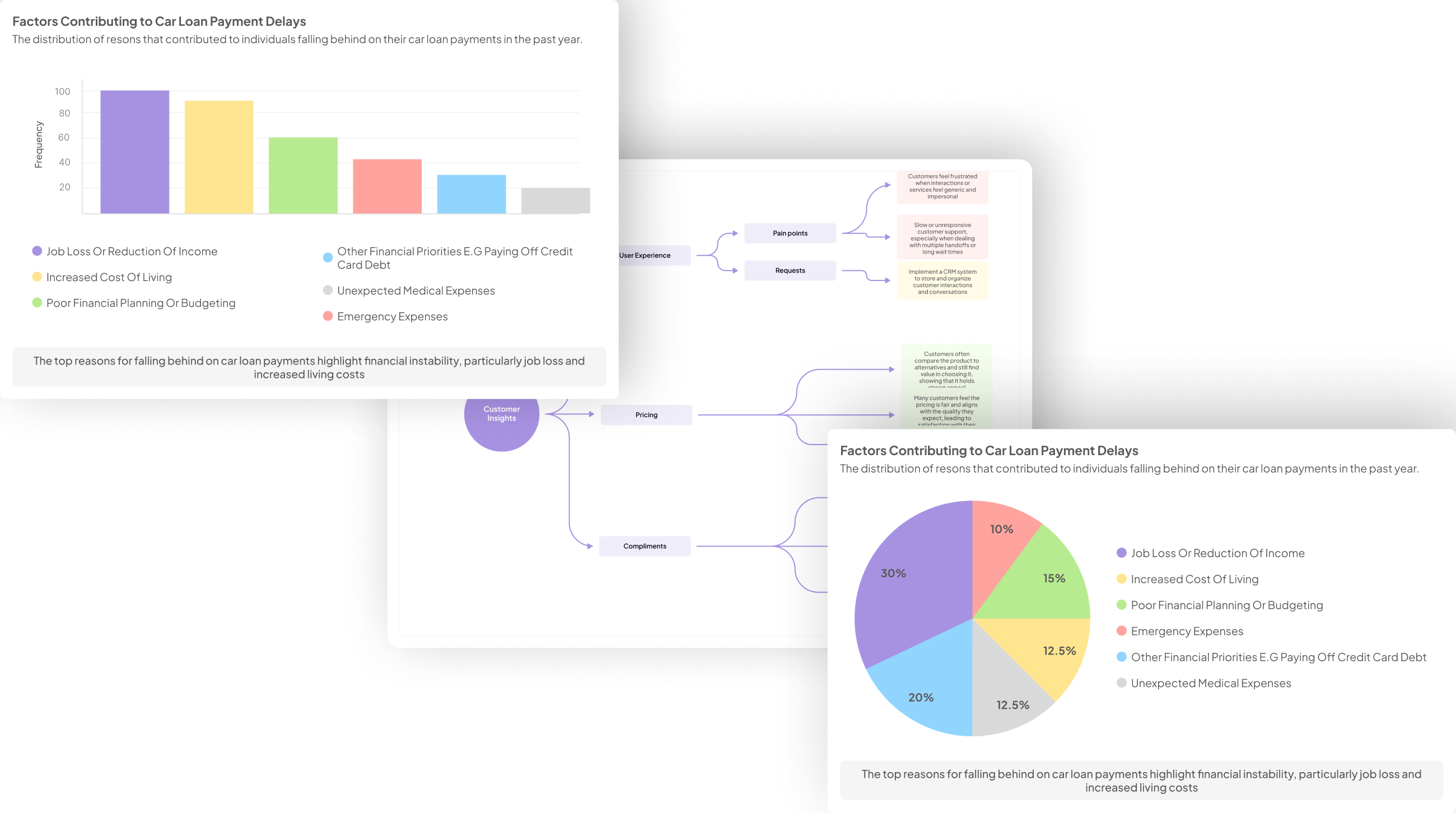
Generate visualizations from your qualitative data. At Scale.

Looking ahead, the future of Stochastic Value Estimation holds promising potential. Continued innovations in machine learning and data processing are expected to further enhance its applicability. As researchers adopt these advancements, the ability to model complex scenarios will improve, providing deeper understanding and guidance for policy formulation. Embracing these changes will enable practitioners to respond more adeptly to emerging challenges in their fields.